Решение в Linux обыкновенных дифференциальных уравнений

Оригинал: Solving ODEs on Linux
Автор: Joey Bernard
Дата публикации: Mar 19, 2015
Перевод: Н.Ромоданов
Дата перевода: апрель 2015 г.

Многие задачи в науке и технике моделируются с помощью обыкновенных дифференциальных уравнений. Обыкновенным дифференциальным уравнением является уравнение, которое представляет собой функцию от одной независимой переменной и ее производных. Это означает, что практически любую систему, которая изменяется с течением времени, можно смоделировать с помощью обыкновенных дифференциальных уравнений, начиная от небесной механики и расчета скорости химических реакций и до экологии и моделирования народонаселения.

Благодаря подобной вездесущности, многие инструментальные средства, предназначенные для решения и анализа обыкновенных дифференциальных уравнений, разрабатывались на протяжении многих лет. В этой статье я расскажу об одном из таких из инструментов, который доступен на Linux: Model Builder. Проект размещен на SourceForge, так что вы всегда можете собрать его из исходников, но в большинстве дистрибутивов этот пакет уже должен присутствовать. В дистрибутивах, основанных на Debian, вы можете установить его с помощью следующей команды:

sudo apt-get install model-builder

Эта команда также установит несколько модулей Python, которые нужны для выполнения некоторых задач. Если вы решите собирать пакет из исходных кодов, то вам потребуется разрешать эти зависимости самостоятельно.

Вместе с исходным кодом предлагается каталог с примерами. Вы можете воспользоваться ими в качестве отправной точки и получить некоторые представления о том, что вы можете делать с помощью пакета Model Builder. Документации немного, поэтому вам для того, чтобы почувствовать те преимущества, которые предоставляет пакет Model Builder, возможно, потребуется во всем покопаться самостоятельно.

Чтобы запустить пакет Model Builder, вы можете либо выбрать его в меню в среде вашего рабочего стола, либо в окне терминала выполнить команду PyMB. Когда будет открыто главное окно, то вам будет предложен шаблон, с помощью которого вы можете определить задачу, которую вы анализируете (рис.1). На главной панели, которая называется Differential Equations (Дифференциальные уравнения), вы можете определить набор обыкновенных дифференциальных уравнений, которые вы пытаетесь решить. Общий вид этих уравнений будет следующим dy/dt = f(y,t).

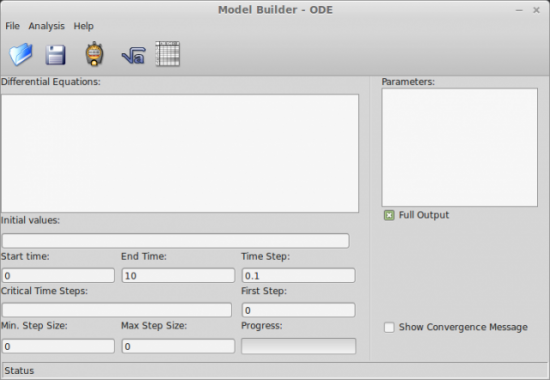
Рис.1. После того, как пакет Model Builder будет запущен, вы сможете задать несколько параметров и определить уравнения, которые вы хотите проанализировать

Если ваша система описывается дифференциальными уравнениями другого вида, то вы всегда можете перезаписать их в виде системы обыкновенных дифференциальных уравнений. Когда вы описываете вашу систему в Model Builder, то вам нужно написать только правую часть уравнения. Поскольку в Model Builder для выполнения сложной работы используется Python, то в этом уравнении могут быть, по существу, любые функции или выражения, которые понимает пакет NumPy.

Т.к. пакет Model Builder предназначен для обработки систем уравнений, вам необходимо указывать часть у в виде элемента списка. Поэтому переменная у первого уравнения обозначается как y[0]; переменная у второго уравнения обозначается как y[1] и так далее. Они называются переменными состояния.

Правая часть уравнения записывается в специальном окне, в котором вы можете указать любые нужные вам параметры, по одному в каждой строке. Ими можно пользоваться в окне уравнения, где вы их можете обозначать как p[0], p[1] и так далее. Если вы хотите где-нибудь в параметрах или в уравнениях указывать значение времени, то просто используйте переменную t.

Поскольку в основе системы используется Python, то для того, чтобы определять более сложные структуры, можно даже пользоваться лямбда функциями. Чтобы узнать о всех имеющихся вариантах, вы можете ознакомится с документацией, которая есть на сайте NumPy.

Под этими двумя панелями вы можете определить прочие параметры, которые будут использоваться в вашей задаче. В поле начальных значениях Initial values вы можете ввести начальные значения для каждого параметра состояния в момент времени t=0. Параметры должны быть разделены пробелами и следовать в том порядке, в каком они расположены в формулах, приведенных в панели уравнений.

Под начальными значениями вы можете ввести начальное время, конечное время и временной шаг, которые будут использованы в решении. Входное поле критически важных шагов, как правило, остается пустым, так что давайте сейчас не будем его заполнять. В поле первого шага указывается размер первой шага. Чтобы размер шага определялся автоматически, вы, как и обычно, должны оставить это значение равным 0. В полях ввода минимального и максимального размера шага можно задать соответствующие значения, которые будут использованы в алгоритме с переменным размером шага. Чтобы эти значения определялись автоматически, вы также должны оставить их значения равными 0. Помеченное флажком поле полной выдачи позволит вам выдать в таблице результатов максимальное количество полезной информации о процессе вычислений.

После того, как все будет введено, вам останется только нажать кнопку Пуск и начнется процесс вычислений. Если это система, с которой вы хотите работать с будущем, то вы можете выбрать пункт меню File→Save (Файл → Сохранить) и сохранить модель в файле. Это файл в формате XML, так что вы можете, если захотите, отредактировать его с помощью текстового редактора. Когда вы будете готовы продолжать с ним работать с ним, вы можете загрузить его, выбрав в меню File → Open (Файл → Открыть).

После того, как вычисления будут произведены, а это для простых задач может произойти быстро, появится окно результатов (рис.2). Это окно графика обрабатывается с помощью библиотеки matplotlib, так что вы можете работать с ним точно также, как и с любым другим окном matplotlib. В нем можно воспользоваться режимом панорамирования, масштабированием или можно изменить внешний вид выдаваемого графика. Вы также можете сохранить изображение полученного графика в файле в одном из нескольких форматов.

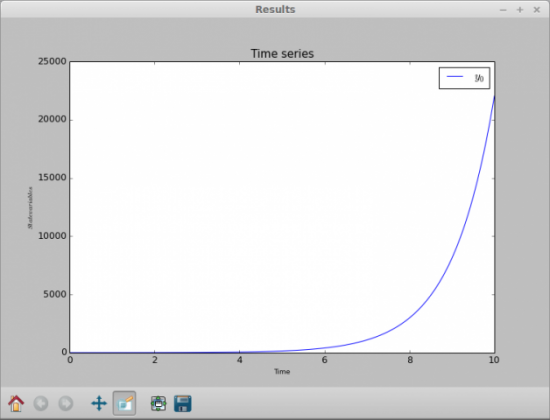
Рис.2. После того, как решение задачи будет закончено и будет получен результат вычислений, появится окно, в котором будет отображен график результата вычислений.

Давайте возвратимся к главному окну и посмотрим на некоторые другие имеющиеся в нем возможности. Если вы щелкните по иконке Show equations (Показать уравнения), то появится окно, в котором можно увидеть набранные уравнения (рис.3). Кроме этой иконки есть иконка Results (Результаты). Если щелкнуть по ней мышкой, то появится таблица результатов всех ваших вычислений (рис.4). В столбцах, кроме всего прочего, указываются также время, значение y[0] и размеры шага. Вы можете выбрать несколько столбцов, если будете удерживая нажатой клавишу Ctrl щелкать мышкой по заголовкам столбцов. Затем для того, чтобы для них в новом окне построить график, щелкните по иконке Plot (Диаграмма). Вы можете получить спектрограмму для одного из столбцов — для этого выберите один из них и щелкните по иконке Spectrum (Спектрограмма). Появится два новых окна: в первом будет изображен спектр для выбранного столбца(рис 5), а во втором — его спектрограмма (рис 6).

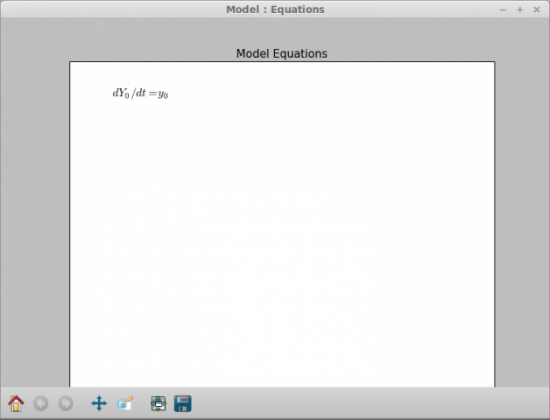
Рис.3. Вы всегда можете посмотреть, как выглядят ваши уравнения

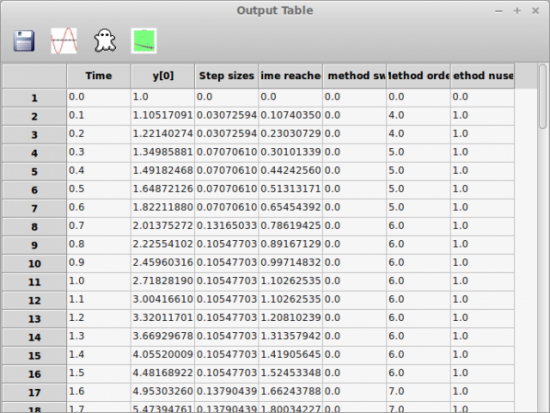
Рис.4. Вы всегда можете получить результаты всех ваших вычислений и использовать их для дальнейшего анализа

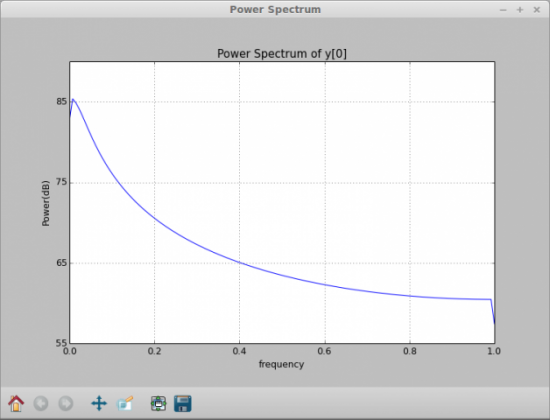
Рис.5. Вы можете построить спектр для любого столбца результатов ваших вычислений

Рис.6. Вы также можете сгенерировать спектрограмму ваших результатов

Последним доступным инструментом является вейвлет-преобразование. После того, как вы выберите столбец, вы можете применить к данным непрерывное вейвлет-преобразование. Затем, когда завершите работать с Model Builder, вы можете сохранить данные, находящиеся в окне с таблицей, в файла, значения в котором будут разделены запятыми (формат CSV). Потом вы можете импортировать его в другие инструментальные средства, например, в R для дальнейшего анализа.

Теперь, когда вы знакомы с возможностями пакета Model Builder, вы, скорее всего, воспользуетесь им, когда потребуется решать задачи в обыкновенных дифференциальных уравнениях. В нем сравнительно простой интерфейс, позволяющий с помощью инструментальных средств языка Python получать численные решения обыкновенных дифференциальных уравнений. Несмотря на то, что есть другие более мощные инструментальные средства, пакет Model Builder хорошо вписывается в нишу, позволяющей быстро экспериментировать с различными уравнениями и проверять различные идеи.

http://rus-linux.net/MyLDP/soft/solving-odes-in-linux.html